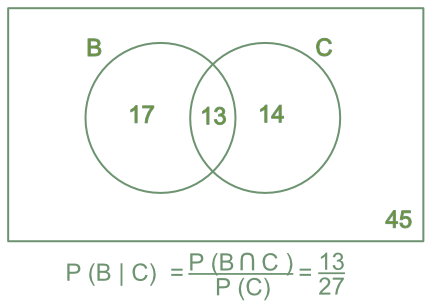Probability Venn Diagram Formulas

Let us write the formula for conditional probability in the following format hspace100pt pa cap bpapbapbpab hspace100pt 15 this format is particularly useful in situations when we know the conditional probability but we are interested in the probability of the intersection. Problem solving using venn diagram is a widely used approach in many areas such as statistics data science business set theory math logic and etc. Pa020201007057 in venn diagram pa is pictorially represented as calculation of pb probability of b is represented as pb pb is calculated by adding all values of the set b.

wiring diagram for chevy impala wedding certificate texas wiring harnes 2002 cadillac sl what program do i need to make a resume yoni massage certification wire diagram for 2004 mustang gt wix fuel filter suppressor ar 15 wedding hashtag sign template free

Calculating Probability Using Venn Diagrams

Venn Diagrams Read Probability Ck 12 Foundation

Probability Calculations Using Venn Diagram

This is definitely not the case however.

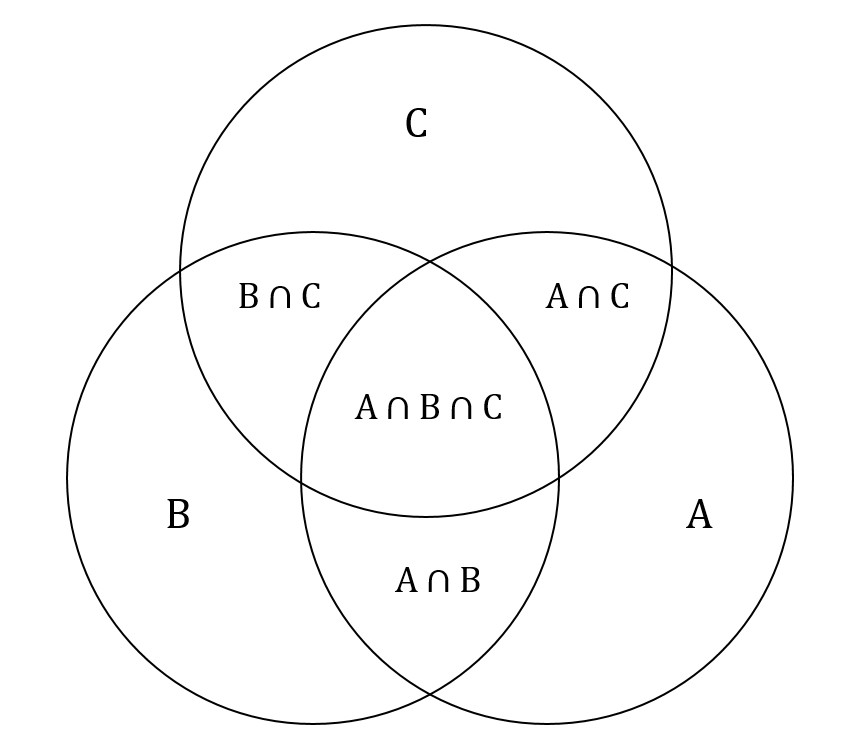
Probability venn diagram formulas. We can interpret this formula using a tree diagram such as the one shown in figure 123. Joint union complement and conditional probabilities examples included. Venn diagrams and formulas. N a b na n b n a b n a b c na n b n c n a b n b c n c a n a b c and so on where n a number of elements in set a.

Venn diagrams and the overlapping set equation. Pb 005005001003 014 in venn diagram pb is pictorially represented as. This lesson covers how to use venn diagrams to solve probability problems. This video demonstrates how to solve probability questions using a venn diagram.

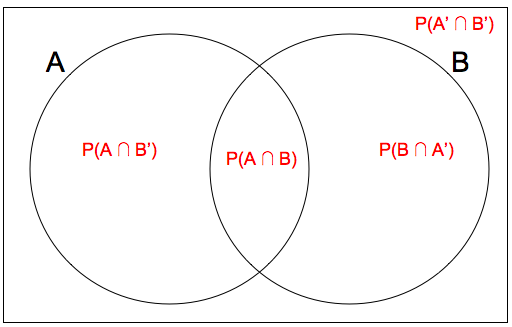
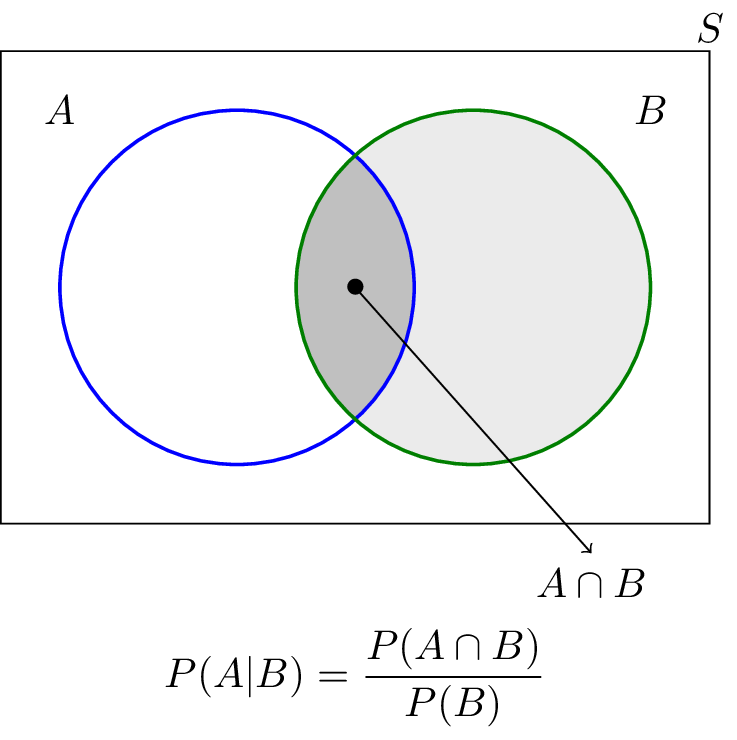
Chain rule for conditional probability. Lets take a look at some basic formulas for venn diagrams of two and three elements. Probability of a is represented as pa pa is calculated by adding all values of the set a. In question 1 the two events drawing a heart drawing a queen are independent.

The simplest and most typical venn diagram depicts two overlapping circles. For the first question you can say that while in the second problem you cannot do that. Sometimes people think that fancy notation and formulas must always be relied upon to solve probability problems. Sometimes visuals such a venn diagrams are good enough to help you get the right answers.

In question 2 the two events rolling a number less than 4 rolling an odd number are dependent. The best way to explain how the venn diagram works and what its formulas show is to give 2 or 3 circles venn diagram examples and problems with solutions. Venn diagram also known as euler venn diagram is a simple representation of sets by diagrams. These diagrams can also provide intuitive insight into the nature of the problems.

Sets a creatures with two legs and b creatures that can fly this example involves two sets. Venn diagram representing mathematical or logical sets pictorially as circles or closed curves within a rectangle. Formulas for venn diagrams definitions. A venn diagram or set diagram is a diagram that shows all possibilities of overlap and non overlap of two or more sets.